一、( 25 分)简要回答以下问题:
1 、某种元素晶体具有 6 角密堆结构,试指出该晶体的布拉伐( Bravais )格子类型和其倒格子的类型。
2 、某元素晶体的结构为体心立方布拉伐格子,试指出其格点面密度最大的晶面系的密勒指数,并求出该晶面系相邻晶面的面间距。(设其晶胞参数为 a )。
3 、具有面心立方结构的某元素晶体,它的多晶样品 x- 射线衍射谱中,散射角最小的三个衍射峰相应的面指数是什么?
4 、何谓费米能级和费米温度?试举出一种测量金属费米面的实验方法。
5 、试用能带论简述导体、绝缘体、半导体中电子在能带中填充的特点。
二、( 15 分)回答以下问题:
1 、阐述晶格中不同简正模式的桥梁波之间达到热平衡的物理原因。
2 、晶格比热理论中德拜( Debye )近似在低温下与实验符合的很好,物理原因是什么?
3 、晶体由 N 个原子组成,试求出德拜模型下的态密度、德拜频率的表达式,并说明德拜频率的物理意义。
三、( 20 分)设有一维双原子链,两种原子的质量分别为 M 和 m ,且 M>m ,相邻原子间的平衡间距为 a ,只考虑最近邻原间的相互作用,作用力常数为 β ,在简谐似下,考虑原子沿链的一维振动。
1 )求格波简正模的频率与波矢间的关系 ω ( q )
2 )证明波矢 q 和 ![]() (其中 m 为整数)描述的格波是全同的
(其中 m 为整数)描述的格波是全同的
3 )在 M>>m 的极限情形,求色散关系 ω ( q )的渐近表达式
四、( 20 分)推导简立方晶格中由原子 S 态 ф S ( r )形成的能带:
1 、写出描述 S 态晶体电子波函 数的 Bloch 表达式 2 、写出在最近邻作用近似下, 由紧束缚法得到的晶体 S 态电子能 量表达式 E ( k ) 3 、计算如图 Г, X,R点晶体电 子能量 4、指出能带底与能带顶晶体电 子能量,其能带宽度等于多少? 5、画出原子能级分裂成能带示 意图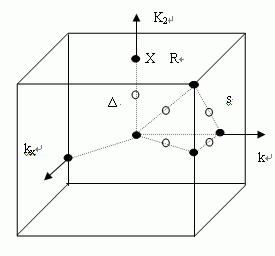
五、( 20分)金属钠是体心立方晶格,晶格常数 ![]() ,假如每一个锂原子贡献一个传导电子而构成金属自由电子气,试推导 T=OK时金属自由电子气费米能表示式,并计算出金属锂费米能。
,假如每一个锂原子贡献一个传导电子而构成金属自由电子气,试推导 T=OK时金属自由电子气费米能表示式,并计算出金属锂费米能。
![]()
