一、（ 8 分）假设事件 A 与 Bi （ i=1,2,...,n) 相互独立，其中 B1,B2,...,Bn 两两不相容。证明 A 的补集与 B1+B2+...+Bn 相互独立。
二、（ 10 分）已知随机变量 X 的分布函数为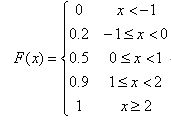 
试求将 X 标准化之后得到的变量 Y （即 Y ＝ (X － μ)/σ ，其中 μ 和 σ 分别表示 X 的期望和标准差）的分布函数。
三、（ 12 分）设（ X,Y) 的联合密度函数为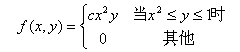 
其中， c 是某个待定常数。
试求： 1 、 P ｛ X ＋ Y ＞ 1 ｜ X>0};
2 、 X 与 Y 是否相互独立。
四、（ 8 分）在某个公共汽车站一小时内等候的人数服从泊松（ Poisson) 分布，根据以往大量的随机观测平均每小时有 36.73 人候车，请问一小时内最可能在此车站候车的人数是多少？
五、（ 12 分）设总体服从区间 [0,θ] 上（ θ ＞ 0 ）的均匀分布， X1,X2,...,Xn 是从中抽取的一个简单随机样本。
试求： 1 、 θ 的最大似然估计；
2 、 θ 的一个置信度为 1-α 的置信区间 (α >0) 。
六、（ 10 分）某个厂家生产的 10 件产品中次品的个数未知。甲从中有放回地抽取了 n 次，结果没有抽到次品，并由此接受这 10 件产品中没有次品的假设。请甲可能会犯什么类型的错误？为了使得甲犯该类型错误的最大概率不超过 60% ，他至少需要抽取多少次？ 
八、 (6 分 ) 试证明：若线性规划有两个不同的最优解，则它有无穷多个最优解。
九、 (12 分 ) 线性规划的目标函数是 Max z ，在用标准的单纯型法求解的过程中，得到下表 ( 其中 a,b 是常数，部分数据有缺失 ) ：
C | 2 | 5 | 8 | 0 | 0 | 0 | ||
Cb | Xb | B | X1 | X2 | X3 | X4 | X5 | X6 |
X6 | 20 | 0 | 3 | 0 | ||||
X2 | B | A | 1/2 | |||||
X4 | 8 | -2 | -1 | 1 | ||||
Cj-Zj | -2 | |||||||
1) 在答卷纸上画出此单纯型表，并在所有空格中填上适当的数 ( 其中可含参数 a,b) 。
2) 判断以下四种情况在什么时候成立，并简要说明理由。
(1) 此解为最优解？请写出相应的基解和目标函数值。
(2) 此解为最优解，此规划又有无穷多最优解？
(3) 此规划有无界解？
(4) 此解不是最优解，且能用单纯型法得到一下一个基解。
十、 (12 分 ) 某地区有三个煤矿，专供四个城镇之用。已知各煤矿与各城镇之间的运输费用矩阵如下 ( 单位：元 / 吨 ) ： 
。已知三个煤矿的产量分别为 25000 吨， 18000 吨， 17000 吨；四个城镇的需求量分别为 12000 吨， 15000 吨， 18000 吨， 24000 吨。若不能满足需求，各城市的最低需求分别为 8000 吨， 10000 吨， 12000 吨， 15000 吨。
(1) 试建立使本地区四城镇煤炭运费最小的线性规划模型。
(2) 写出此线性规划的对偶规划
