一、（ 10 分）

设质量为 m 的粒子在一维无限深势阱中运动

试用 de Broglie 的驻波条件，求粒子能量的可能取值。

二、（ 10 分）

设一个质量为 m 的粒子束沿正 x 方向以能量 E 向 x=0 处的势垒运动

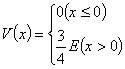
试用量子力学的观点回答：在 x=0 处被反射的反射系数是多少？

三、（ 20 分）

1 、在坐标表名胜中写出一维量子体系的坐标算符 和动量算符 ，并推导其间的对易关系。

2 、在动量表象中做 1 所要求做的问题。

四、（ 20 分）

设一个微观粒子在球对称的中心势场 中运动，且处于一个能量和轨道角动量的共同本征态。

1 、在球坐标系中写出能量本征态波函数的基本形式，写出势能 在此态中平均值 〈 V〉的表达式，并最后表示成径向积分的形式。

2、设V(r)为r的单调上升函数（即对任意r, ）。试证明：对任意给定的 r 0 ，均有

，

其中 R(r)是径向波函

五、（ 20分）

设一个质量为 m的微观粒子的哈密顿量不显含时间，试证明：在能量表象中有

其中 E 为能量， x 为坐标。

六、（ 20 分）

设一微观体系的哈密顿 H=H 0 +H ‘ ，其中 H ' 为微扰。在一个由正交归一函数作为基的表象中。

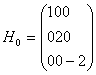
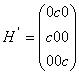
其中 c 为常数

1 、求 H 的精确本征值

2 、求 H 的准确到微扰的二级修正的本征值