积分考查综合性强,是高等数学中的核心计算,也是考研数学考查的重中之重,所占比重最大,大题2-3个小题3-4个。本文将梳理不定积分、定积分及二重积分的基本计算思路及方法,目的是使知识系统化。
一、不定积分
不定积分的计算是整个积分运算的基础,定积分、重积分的计算都是依赖于此。因此掌握不定积
分的计算方法和思路非常重要。
不定积分计算的根本是最基本的积分公式,我们将这些公式分为两种,一种是直接将常用的求导公式反过来得到的积分公式:
如![]() 等
等
另一种是在计算积分的过程中得到的一些比较常用的公式,例如:
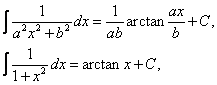
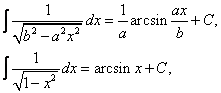
![]()
![]()
这些公式在今后的计算中经常用到,所以也总结在基本积分公式中,需要同学们记忆并熟练应用。在基本公式的基础之上,掌握常见的积分法即可正确解题,需要清楚的是,不管是何种积分方法,最终都是转化为用基本积分公式解题。
常见的积分法:第一类换元积分,又称为凑微分法,用来解决被积函数中同时存在原函数与导函数的情况,基本思想是![]() ;第二类换元积分是与第一类换元法相反的思路,在计算过程中应用得很频繁,基本思想是
;第二类换元积分是与第一类换元法相反的思路,在计算过程中应用得很频繁,基本思想是![]()
![]() ;分部积分法主要解决两类不同类型的函数的乘积形式的积分,尤其是含有反三角函数、对数函数时的积分,基本思想是
;分部积分法主要解决两类不同类型的函数的乘积形式的积分,尤其是含有反三角函数、对数函数时的积分,基本思想是![]() ,关键点是
,关键点是![]() 、
、![]() 的选取。
的选取。
常见的基本题型包括:有理函数的积分;可化为有理函数的积分(包括:三角有理式、指数有理式);根式的处理;分部积分法的使用等。
二、定积分
定积分的计算包含两方面:一、基本思路是牛莱公式,利用不定积分的解题方法来计算;二、利用对
称区间及函数的基本性质来解题,主要是运用函数的奇偶性。
1、利用不定积分的计算方法
1)换元法
定理:设函数![]() 在区间
在区间![]() 上连续,函数
上连续,函数![]() 满足条件:
满足条件:
ⅰ![]()
ⅱ![]() 在区间
在区间![]() 上具有连续导数,其值域
上具有连续导数,其值域![]()
则有![]()
注意:上下限要对应;
2)分部积分法
![]() 。
。
出现抽象函数的导数或二阶导数,一律使用分部积分,例如设![]() 有一个原函数
有一个原函数![]() ,求
,求![]() 。
。
2、对称区间上函数定积分的计算
1)利用奇偶性
设![]() 在区间
在区间![]() 上可积
上可积
如果![]() 是偶函数,则有
是偶函数,则有![]() ;
;
如果![]() 是奇函数,则有
是奇函数,则有![]() 。
。
2)被积函数本身无奇偶性,直接计算积分又难算时考虑变量代换,令![]() ,例如
,例如![]() 。
。
特别地,分段函数的积分利用区间可加性先分段再计算,如果函数![]() 的在区间
的在区间![]() 上的解析式为
上的解析式为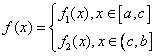 ,则
,则![]() ;当被积函数中含有绝对值,最大值
;当被积函数中含有绝对值,最大值![]() 或最小值
或最小值![]() 符号,或是极限式时,其本质上也是分段函数。因此,需要先写出被积函数的分段解析式,再分段计算。
符号,或是极限式时,其本质上也是分段函数。因此,需要先写出被积函数的分段解析式,再分段计算。
三、二重积分
计算二重积分的基本思路是将其化作累次积分(也即两次定积分),要把二重积分化为累次积分,有两个主要的方式:一是直接使用直角坐标,二是使用极坐标。这是我们计算二重积分的两个主要的武器。
首先,对直角坐标来说,主要考点有两个:一是积分次序的选择,基本原则有两个:一是看区域,选择的积分次序一定要便于定限,说得更具体一点,也就是要尽量避免分类讨论;二是看函数,要尽量使第一步的积分简单,选择积分次序的最终目的肯定是希望是积分尽可能地好算一些,实践表明,大多数时候,只要让二重积分第一步的积分尽可能简单,那整个积分过程也会比较简洁,所以我们在拿到一个二重积分之后,可以根据它的被积函数考虑一下第一步把哪个变量看成常数更有利于计算,从而确定积分次序。
二是定限,完成定限之后,二重积分就被化为了两次定积分,就可以直接计算了。
关于极坐标,我们主要关注三个问题:
首先是转换公式:![]() ,
,![]() 。这里要注意的是将
。这里要注意的是将![]() 转化为
转化为![]() 之后前面要乘上
之后前面要乘上![]() ,这是因为
,这是因为![]() 表达的是指教坐标下的面积元,而在极坐标下的面积元的表达式为
表达的是指教坐标下的面积元,而在极坐标下的面积元的表达式为![]()
其次是极坐标的适用范围,也即什么情况下要想到利用极坐标计算。这里基本原则也有两个:一是看函数,始于极坐标的被积函数最佳形式是![]() ,一般情况下,要求可以减弱,只要被积函数中含有
,一般情况下,要求可以减弱,只要被积函数中含有![]() 就可以考虑使用极坐标进行计算;二是看区域,如果积分区域为圆或是与圆相关(环形、扇形、或者边界的某一部分为圆弧),就可以考虑使用极坐标。
就可以考虑使用极坐标进行计算;二是看区域,如果积分区域为圆或是与圆相关(环形、扇形、或者边界的某一部分为圆弧),就可以考虑使用极坐标。
最后一个问题是定限方法,极坐标不存在积分次序的问题,肯定是先对![]() 积分(先对
积分(先对![]() 积分的大部分都很复杂),所以,确定要用极坐标计算之后,直接定限即可。
积分的大部分都很复杂),所以,确定要用极坐标计算之后,直接定限即可。
以上是我们计算二重积分的主体思路,在此基础之上,我们还可以利用对称性,它在二重积分的计算中虽然属于辅助性的技能,但如果恰当使用的话,还是可以明显地简化计算。
二重积分中的对称性分为两种:一是奇偶性,二是轮换对称性。一般来说,对称性应该使用在拿到一个二重积分之后的第一步,只要积分区域关于某坐标轴是对称的,就要先检验被积函数是否具有相应的对称性,尤其要注意有没有奇函数,以尽可能地简化计算。
以上是对考研高等数学积分部分的一个简单分析,希望能够对2014年考研的同学起到一定的作用,用有限的时间取得最好的成绩。最后跨考教育数学教研室全体教师祝广大考生复习顺利,考研成功
