定积分的应用是考试的重点内容，针对这部分重要内容进行一下深度解析，万学海文在此帮助考生分析一下定积分应用的命题规律。

　　定积分的应用主要是以微元法为基础，而微元法又是以定积分的定义为基础。所以，分割、近似、求和、取极限是计算一些几何量和物理量的指导思想。

　　定积分及其应用这部分内容在历年真题的考察中形式多样，可以以客观题的形式出现，也可以在解答题中出现，并且经常与其它知识点综合起来考察，比如与极限、导数、微分中值定理、极值等知识点综合在一起出题。

　　在这部分需要重点掌握用微元法计算平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等。。而对于数三只要求会计算平面图形的面积和旋转体的体积就可以了。其中求旋转体的体积以及微积分的几何应用与最值问题相结合构成的应用题是重点常考题型，广大考生应该予以充分的重视。

　　对于定积分的应用部分，首先需要对微元法熟练掌握。在历年考研真题中，有大量的题是利用微元法来获得方程式的，微元法的熟练应用是倍受出题老师青睐的知识点之一；但是由于微元法这种方法本身有思维上的跳跃，对于这种灵活有效的方法必须通过足量的练习才能真正体会其思想。在此结合函数图像与对应的微元法核心式来归纳微元法的三种常见类型：

　　1.薄桶型。

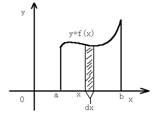
　　本例求的是由平面图型a≤x≤b,0≤y≤f(x)绕y轴旋转所形成的旋转体体积。方法是在旋转体上取一薄桶型形体(如上图阴影部分所示)，则根据微元法思想可得薄桶体积  ,其中是薄桶的高，是薄桶展开变成薄板后的底面积，就是薄板的厚度；二者相乘即得体积。  

　　对  积分可得 。在这个例子中，体现微元法特色的地方在于：a。虽然薄桶的高是个变化量，但却用来表示；

　　b。用表示薄桶的厚度；

　　c。核心式。

　　2.薄饼型。

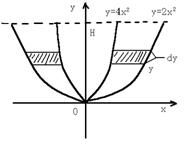
　　本例求的是由抛物线及绕轴旋转形成的高的旋转体体积，方法是取如上图阴影部分所示的一个薄饼型形体，可得微元法核心式 。其中  是薄饼的底面积，薄饼与  旋转面相交的圆圈成的面积是 ,∵，∴；同理薄饼与  旋转面相交的圆圈成的面积是， 二者相减即得薄饼底面积。核心式中的是薄饼的高。这个例子中的薄饼其实并不是上下一般粗的圆柱，而是上大下小的圆台，但将其视为上下等粗来求解，这一点也体现了微元法的特色。

　　3.薄球型。

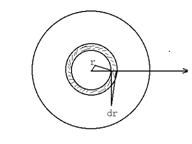
　　本例求球体质量，半径为，密度， 其中指球内任意一点到球心的距离。方法是取球体中的一个薄球形形体，其内径为厚度为，对于这个薄球的体积有，其中是薄球表面积，是厚度。该核心式可以想象成是将薄球展开、摊平得到一个薄面以后再用底面积乘高得到的。由于很小，故可认为薄球内质量均匀，为，则薄球质量，积分可得结果。本例中“用内表面的表面积乘以薄球厚度得到核心式”、“将内的薄球密度视为均匀”体现了微元法的特色。

　　通过以上三个例子谈了一下了对微元法特点的一点认识。这种方法的灵活运用必须通过自己动手做题体会才能实现，因为其中一些逻辑表面上并不符合常规思维，但也许这正是研究生入学考试出题老师喜欢微元法的原因。