极限--微积分学能够建立的基础，在我们考研数学中也占有非常重要的地位，体现在统计28年考研数学的数据，从中看到和极限直接相关的知识点共有7类，每年占10-15分左右，现在，跨考教育数学教研室赵睿老师就极限的相关考点，和大家讨论一下关于极限的学习方法和侧重点。

　　对于极限，我们分为一元函数的极限和多元函数极限，重点在一元函数极限。

　　首先，对于极限的定义，是这1、2年的热点，14年15年都考查了关于极限定义的选择题，这也符合大纲中所说的“理解极限的概念”这一要求。对于极限的定义，大纲不要求用它来求极限，只需要理解定义中的含义。是指任意小的一个正数，是可以任意选取的一个正数，但一般要求不能选的大于极限的一半或是直接要求在(0,1)之间。做题时，取到合适的值往往是关键点。

　　其次，对于极限考查的重点还是如何来求极限。我们总结求极限的方法大致有8种，比如等价无穷小代换、两个重要极限、洛必达法则、泰勒公式求极限 等等。在5年前，重点还是如何用洛必达法则求极限，但近几年，重点越来越倾向于用泰勒公式来求极限。用泰勒公式求极限的最大优势，就是把函数转化成多项式 的形式，然后用无穷小的比较，或者“抓大头”的方法来求极限；当然记熟函数的泰勒展开式是前提，大纲要求掌握的由5个函数有

　　。

　　例如：2015年数一(15)题

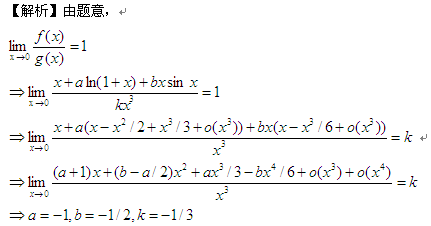
　　此题若用洛必达法则至少用两次，而且还不好计算，用泰勒公式省时又省力。其他求极限的方法，也需要多加练习，才能在考试中游刃有余。