考研数学在公共课中占的分数是很高的，而高等数学又是考研数学中占有很大比重的一门学科。在此，跨考教育吴方方老师就考研数学高数中出现的恒等变形方法和大家探讨其三种分类形式。

　　第一种形式；“加减乘除”。所谓的加减乘除就是在所要求的式子中加一项，然后再减一项，使得所得到的式子和原式恒等。这种情况的使用在极限和求导数的时候都出现过。

图1

　　导数中，用到导数定义时，往往也要加一个减一个来凑成导数数想形式，这里就不多列举了。

　　第二种形式：“令一个比较复杂的式子=t”。积分是考研中常考的知识点，而对于不定积分和定积分的计算是要求我们必须掌握的。在求积分时，往往 会碰到比较复杂的部分。所以对于这种情况我们就把那个比较复杂的部分令成t，也就是积分中的变量替换。这种“举重若轻”的思想形式也就体现了我们所讲的恒 等变形方法。

　　第三种形式：“先积后导和先导后积”。这种情况如其名，就是先求积分后求导数或者是先求导数然后再求积分，使得作用后的式子与原式是相等的。这 种形式是恒等变形方法中的比较高级的形式了，当然也是很难的一种形式。它主要用在我们高等数学中的幂级数求和函数或者和函数展开成幂级数的形式。

　　对于高等数学中的无穷级数这章是数一和数三要考的内容，而数学二的同学不考这一章节。我们知道无穷级数分为常数项级数和函数项级数，而函数项级 数中的幂级数是我们考试的重要内容。其中幂级数的收敛域和它的和函数的求法，以及和函数展开成幂级数，这些是数一和数三的同学必须掌握的内容。在幂级数求 和函数以及和函数展开成幂级数时，我们往往是要用到先积分后导，和先导后积分的恒等变形方法的。

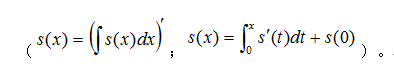图2