1）基于四进制的线性四叉树编码

  编码的目的是给四叉树的结点赋于唯一的地址码，即Morton码。为便于计算可用四进制数来标记，称为四进制线性四叉树编码。           

四进制代码： MQ=2×Ib+Jb Ib和Jb 是二进制行、列号

2）基于十进制的线性四叉树编码

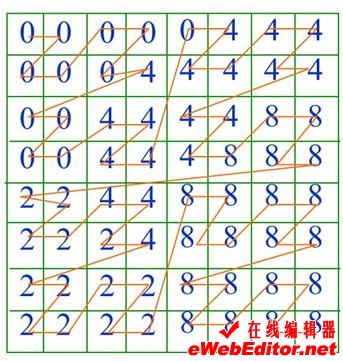
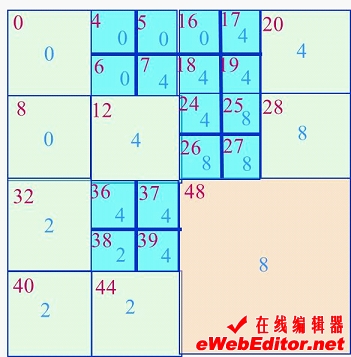
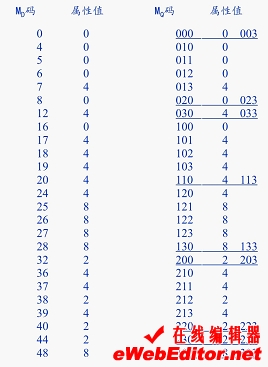
  四进制码虽然直观，但支持四进制码的计算机语言几乎没有。转换再加上排序费时费力，极不实用。所以通常采用由下而上的递归合并法建立四叉树，并用十进制的Morton码(简称MD码)作为线性四叉树的地址码。该码实际上就是自然数码。

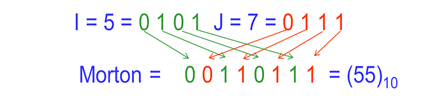
MD码的计算可;按位操作法进行：首先将二维栅格的行列号(十进制)转化成二进制；然后按各位的顺序交叉放入Morton码变量中，即可得到线性四叉树的地址码。

例如，某栅格单元的行号  I=5，列号 J=7， Morton码的计算如下图所示：       

（一）泰森多边形

在地图上作所有相邻观测点连线的垂直平分线，由这些平分线构成的包围每个观测点的多边形就是所谓的泰森多边形。在泰森多边形的边界上任取一点，到相邻两个观测点的距离是相同的，而多边形内的任意点到该多边形内的观测点距离最近。

（二）几种栅格编码方法的特点

直接栅格编码：简单直观，是压缩编码方法的逻辑原型（栅格文件）；

链码：压缩效率较高，已接近矢量结构，对边界的运算比较方便，但不具有区域性质，区域运算较难；

游程长度编码：在很大程度上压缩数据，又最大限度的保留了原始栅格结构，编码解码十分容易，十分适合于微机地理信息系统采用；

块码和四叉树编码：具有区域性质，又具有可变的分辨率，有较高的压缩效率，四叉树编码可以直接进行大量图形图象运算，效率较高，是很有前途的编码方法。

（三）决定栅格单元代码的方法

（1）面积占优法：以占栅格最大的地物类型或现象特征决定栅格代码。

（2）长度占优法：当覆盖的格网过中心部位时，横线占据该格中的大部分长度的属性值定为该栅格的代码。

（3）重要性法：根据栅格内不同地物的重要性，选取最主要的地物类型决定相应的栅格单元代码。对于特别重要的地理实体，其所在的区域尽管面积很小或不在中心，也采取保留的原则，台稀有金属矿区域等。

（4）中心点法：用处于栅格中心处的地物类型或现象特性决定栅格代码。

（四）空间数据分类

根据系统功能及国家规范和标准，将具有不同属性或特征的要素区别开来的过程，以便从逻辑上将空间数据组织为不同的信息层，为数据应用做准备。

具体分类时：

1）首先根据图形原则，将空间数据分为点、线、面三种类型；

2）根据对象原则，例如河流和道路，同为线状要素，但分属于不同的地理对象，应分为不同的类。

（五）空间数据的编码

指将数据分类的结果，用一种易于计算机和人识别的符号系统表示出来的过程。编码的结果是形成代码。

目的：提供空间数据地理分类和特征描述，便于数据输入、存储与管理以及系统间的数据交换和共享。

（六）空间数据元数据的内容

(1) 对数据集的描述

描述数据集中数据项、数据来源、数据所有者、数据生产历史等；

(2) 对数据质量的描述

描述数据的精度、数据的完整性、数据分辨率、比例尺等；

(3) 对数据转换方法和处理信息的描述

描述数据的转换方法等

(4) 对数据更新和集成等的说明

如数据更新的时间、原因等。

八、空间插值

1、概念

空间插值是用已知点的数值来估算其他点的数值的过程。在GIS应用中，空间插值主要用于估算出栅格中每个像元的值。因此，空间插值是将点数据转换成面数据的一种方法，目的在于使点数据也能用于空间分析和建模中。

控制点是已知数值的点，也称为已知点、样本点或观测点。控制点提供了为空间插值建立插值方法(如数学方程)的必要数据。控制点的数目和分布对空间插值精度的影响极大。

2、空间插值的分类

    空间插值有多种分类方法。

    第 一，它可以分成全局和局部拟合法。全局插值法利用现有的每个已知点来估算未知点的值。而局部插值法则是用己知点的样本来估算未知点的值。由于这两种方法的 区别是用于估算的控制点数目不同，因此，可以将从全局到局部看作是尺度不同的连续统一体。从概念上看，全局插值法用于估算表面的总趋势，而局部插值法用于 估算局部或短程变化。在许多情况下，在估算某个点的未知数值时，局部拟合法比整体拟合法更有效。因为，远处的点对估算值的影响很小，在有些情况下甚至会使 估算值失真。此外，局部拟合法还因计算量小而更受青睐。

    第二，空间插值方法可以分为精确和非精确插值法。对某个数值已知的点，精确插值法在该点位置的估算值与该点已知值相同。换句话说，精确插值所生成的面通过所有的已知点。相反。非精确插值。或称为近似插值，估算的点值与该点已知值不同。

第三，空间插值方法可以分成确定性和随机性两种。确定性插值方法不提供预测值的误差检验。随机性插值方法则用估计变异提供预测误差的评价。随机过程假设通常要求用随机性方法。

3、空间插值意义

（1）缺值估计

如何在没有测点的地区得到我们需要的数据？

测点自然或人为的原因，缺少某天或某个时间段的数据。

（2）内插等值线

形象直观的显示空间数据分布

平面制图

（3）数据格网化

以不规则点图元组织的Z变量的数据，并不适合于图形显示，也不适于进行分析。多数空间分析要求将Z值转换成一个规则间距空间格网，或者转换成不规则三角形网。

规则格网数据更好的显示空间数据连续分布

4、一般插值过程

①  内插方法（模型）的选择；

②  空间数据的探索性分析，包括对数据的均值、方差、协方差、独立性和变异函数的估计等；

③  进行内插；

④  内插结果评价；

⑤  重新选择内插方法，直到合理；

⑥  内插生成最后结果。

5、插值方法选择的原则

①  精确性：

②  参数的敏感性：许多的插值方法都涉及到一个或多个参数，如距离反比法中距离的阶数等。有些方法对参数的选择相当敏感，而有些方法对变量值敏感。后者对不同的数据集会有截然不同的插值结果。希望找到对参数的波动相对稳定，其值不过多地依赖变量值的插值方法。

③  耗时：一般情况下，计算时间不是很重要，除非特别费时。

④  存储要求：同耗时一样，存储要求不是决定性的。特别是在计算机的主频日益提高，内存和硬盘越来越大的情况下，二者都不需特别看重。

⑤   可视化、可操作性（插值软件选择）：三维的透视图等。

6、插值验证

（1） 交叉验证

   交叉验证法（cross－validation），首先假定每一测点的要素值未知，而采用周围样点的值来估算，然后计算所有样点实际观测值与内插值的误差，以此来评判估值方法的优劣。 各种插值方法得到的插值结果与样本点数据比较。

（2）“实际”验证

  将部分已知变量值的样本点作为“训练数据集”，用于插值计算；另一部分样点 “验证数据集”，该部分站点不参加插值计算。然后利用“训练数据集” 样点进行内插，插值结果与“训练数据集”验证样点的观测值对比，比较插值的效果。

7、空间插值的数据采样

采样点的空间位置对空间插值的结果影响很大。

1)  理想情况是研究区内均匀布点：但当区域景观存在有规律的空间分布模式时，用完全规则的采样网络可能会得到片面的结果；

2)  完全随机的采样：采样点的分布位置是不相关的，完全随机采样可能会导致采样点的分布不均，一些点的数据密集，另一些点的数据缺少。

3)  规则采样和随机采样的结合方法是成层随机采样，即划分为规则格网，每个格网中的样本数固定，但单个点随机地分布于规则格网内。

8、插值方法

（1）最近邻法

最近邻点法又叫泰森多边形方法。它采用一种极端的边界内插方法—只用最近的单个点进行区域插值（区域赋值）。

泰森多边形按数据点位置将区域分割成子区域，每个子区域包含一个数据点，各子区域到其内数据点的距离小于任何到其它数据点的距离，并用其内数据点进行赋值。

评价：

特征：用泰森多边形插值方法得到的结果图变化只发生在边界上，在边界内都是均质的和无变化的；

适用于较小的区域内，变量空间变异性也不很明显的情况。符合人思维习惯，距离近的点比距离远的点更相似，对插值点的影响也更明显；

最近邻法插值的优点是不需其他前提条件，方法简单，效率高；

缺点是受样本点的影响较大，只考虑距离因素，对其他空间因素和变量所固有的某些规律没有过多地考虑。实际应用中，效果常不十分理想。

（2）算术平均值

算术平均值方法以区域内所有测值的平均值来估计插值点的变量值(Creutin, 1982)。

评价：算术平均值的算法比较简单，容易实现。但只考虑算术平均，根本没有顾及其他的空间因素，这也是其一个致命的弱点，因而在实际应用中效果不理想。

（3）距离倒数权重插值

距离倒数权重插值是一种精确插值方法，它假设未知值的点受近距离已知点的影响比远距离已知点的影响更大。IDW插值的一个重要特征是所有预测值都介于已知的最大值和最小值之间。

参数：

①  权重

权重过高，较近点的影响较大，拟合表面更细致（不光滑）；

权重过低，较远点的影响增加，拟合表面更光滑。缺省值常为 2 。

②  搜索半径

（1）搜索半径－固定

      对固定型半径，搜索距离一定，所有在该半径内的样点参与计算。

可预先设定一个阈值，当给定半径内搜索到的点小于该值时可扩大搜索半径，直到达到该阈值为止。

（2）搜索半径类型－可变

      设定参与计算的样点数是固定的，则搜索的半径是可变的。这样对每个插值点的搜索半径可能都不同，因为要达到规定的点数所需要搜索的区域是不一样的。

③  障碍设置

可利用一线状和面状数据集来限制样点的搜索。线状数据集可作为平坦地表的悬崖或脊状障碍物：只有位于同侧的样点才符合要求。

评价：

优点——简便易行；可为变量值变化很大的数据集提供一个合理的插值结果；不会出现无意义的插值结果而无法解释。

不足——对权重函数的选择十分敏感；易受数据点集群的影响，结果常出现一种孤立点数据明显高于周围数据点的“鸭蛋”分布模式；

全局最大和最小变量值都散布于数据之中。

距离反比很少有预测的特点，内插得到的插值点数据在样点数据取值范围内。

（4）高次曲面插值

高次曲面插值由 Hardy 于1971年首先提出，随后应用于不同的学科。每个样点对插值点的影响都用样点坐标函数构成的圆锥表示，插值点的变量值是所有圆锥贡献值的总和(Caruso,1998)。