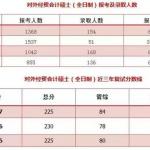
一、考试题型与分值与分布
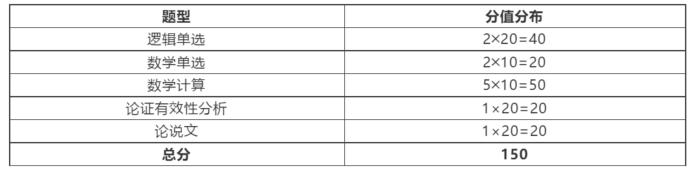
逻辑40分(共20题,每题2分),数学70分,写作(两篇,各20分)。
考试时间3小时,180分钟。
二、复习用书

现在的复习用书越来越多了,每本都有自己有点,复习在于吃透其中的一本或者几本,不要全部都做,消耗太多时间不值得。
注意事项:循序渐进,恰当的时间段做恰当的事情;笨鸟也不能乱飞。
三、复习攻略
逻辑部分(40分):刷题,有需求的可以看视频(老吕、饶思中、赵鑫全的都可以,选择一个你听起来比较耳顺的,讲的方法大同小异,学到家即可);考试要求会做题,概念会不会不重要。
逻辑分册:基本就是习题册,也有少量概念,特点是题多。
逻辑精点:概念+习题,与逻辑分册相比题相对少一点,对概念理解要求高的买精点,直接刷题能解决问题的刷逻辑分册。
1、2,选其中一本;3-6,MBA/MPA/MPAcc历年真题选择其中一本;7、8最好必须买。
这两年逻辑重复率比较高(因为396的逻辑与管综的逻辑题源应该是一致的,都是来自GMAT和GRE),注意刷管综和396的历年逻辑,尤其是管综的(3-6的一本)。
尽早开始,题要每天都做,培养感觉,逻辑需要长时间练习。每天做30题左右即可,雷打不动,长期坚持,时间久了,你就会有很大进步;做错的题,一定要注意标注好,因为题目不只做一遍,建议习题部分,前两次都不要写东西,答案写在一张纸上,到最后一次才在书上写。来回多做几遍。
数学部分(70分):
考试大纲的内容如下:
1、微积分部分:一元函数的微分、积分;多元函数的一阶偏导数;函数的单调性和极值。
2、概率论部分:分布和分布函数的概念;常见分布;期望值和方差。
3、线性代数部分:线性方程组;向量的线性相关和线性无关;矩阵的基本运算
先看课本中大纲要求的部分,然后开始刷题,因为本科学过,捡起来很快。没课本的直接看数学精点,里面有讲解。
经济类联考数学精点(注意别买错成MPACC的数学精点),跨考的60天800题。建议把数学精点和800题刷透,难的题也要会;17年的数学比较难,结果一堆人栽了;18年的也有一道比较难的积分。同时也可以用跨考经济类联考核心笔记+60天800题,这两本书都只出到2014年,之后不再有新版,目前市面出售的都是影印版。
关于课本的使用,如果本科学过数学的,用本科教材捡起来基础知识即可,因为毕竟曾经上过课,捡起来很容易,对比着以上的数学大纲看即可,重点还是60天800题和数学精点。
本科没有学过数学,但想买教材来看的,建议买同济版或者浙大版。具体内容看后文的附件。
写作部分(40分):
到10月再看都来得及,有很强套路。
复习用书:4本选其中一本即可。
微信公众号:专业硕士备考,有一些时事资料可以参考
论证有效性分析,挑一篇文章的逻辑漏洞。基本写作格式一定要掌握,最好有自己写作模板以免大家都用同个板,最后判抄袭就惨了。具体的看买的参考书上,套路特别强。
论说文,类似高中的议论文。一般写成3段论,5股文,有模有样的议论文。禁抒情散文。
模拟试题
11月中旬开始,做周建武老师的《经济类专业学位联考综合能力考试题库》20套题。
四、附件(数学课本复习内容)
高等数学部分(第六版)
第一章 函数、极限与连续
第一节 映射与函数
读7-17页 三、函数
习题1-1:做4、5、6、10、11、12、15、16;第8、9、13记住结论。
第三节 函数的极限
例题看懂即可,不要求自己会证;;四个定理的内容了解
习题1-3:1、2、3、4:第10、11题记住结论,无需证明
第四节 无穷小与无穷大
了解定理1,记住定理2,证明不需要
习题1-4:1、4
第五节 极限运算法则 习题1-5:做第1、2、3、5
第七节 无穷小的比较习 习题1-7:做第1、2、3、4
第八节 函数的连续性和间断点 习题1-8 做第l、2、3、5
第九节 连续函数的运算与初等函数的连续性 习题1-9:1、3、4、5、6
总习题一:2、3、4、5、10、11
第二章 导数与微分
第一节 导数概论
习题2-1:3、4、5、6、7、11、13、14、15、16、17、18、19
第二节 函数的求导法则
例17不做
习题2-2:第4.12不做,其余全做
第三节 高阶导数
会做例题,习题2-3:做1、2、3、4题
第四节 隐函数及由参数方程确定的函数的导数,相关变换率
107页由参数方程确定的函数的导数至111页的内容不看
习题2-4:做第1至4题;
第五节 函数的微分
119页至123页微分在近似计算中的应用不看 习题2-5:做第1至4题
总习题二:1、2、3、5、6、7、8、9、11、14
第三章 微分中值定理与导数的应用
第二节 洛必达法则 习题3-2:1、2、3
第四节 函数的单调性与曲线的凹凸性
习题3-4:1、2、3、4、6、7、8、9、12、13、14
第五节 函数的极值与最大值最小值
例5例6不需要做 习题3-5:第1-10题
总习题三:1、3、10、12、13、17、20
第四章 不定积分
第一节 不定积分的概念与性质
例4不做,其他例题一定掌握 习题4-1:做1、2、5、7
第二节 换元积分法
204页变字体部分包括公式14、15不看,其他例题一定掌握 习题4-2:全做
第三节 分部积分法 例题掌握 习题4-3:全做
第四节 有理函数的积分
会例1、例2、例5、例6、例7、例8
习题44:做第1至11题和第19至22题
总习题四:做第1至第8题、10、12、14、18、19、21、25、26、27、29,
第五章 定积分
第一节 定积分的概念与性质
228页至231页定积分的近似计算部分不看 习题5-1:做3、4、7、13题
第二节 微积分基本公式
例5例6不看 习题5-2:第1、3、4、5、6、9、10、11、12、13
第三节 定积分的换元法与分部积分法
习题5-3:1,7(1)-(12)
总习题五:4、10(1)(4)(6)(7)、11、13
第六章 定积分的应用
第二节 定积分在几何学上的应用
看274页“1、直角坐标情形”;278页“1、旋转体体积,例6,例7”
习题6-2:做第1、2、4、9、12、15(1)(2)
第七、八章不用看
第九章 多元函数微分学
第二节 偏导数
66页例5,例7,例8不做 习题9-2:做1、3、4、6、7、8
第三节 全微分
73页到75页全微分在近似计算中的应用不看:习题9-3:做第1至第4题
第四节 多元复合函数的求导法则
例5不做;习题9-4:做第1-10题
第五节 隐函数的求导公式
86页到89页:二、方程组的情形不看
习题9-5:1、2、3、4、5、8
第八节 多元函数的极值及其求法
例6,例9不看 习题9-8:2、3、4、5
线性代数部分(同济大学第五版课本)
第一章 行列式
§4对换(可不看)
§5行列式的性质 记住结论(证明不看),其余全看
习题一:做1、3、4、5、9、11、12
第二章 矩阵及其运算
§1矩阵 从30页例1起到本节最后 可不看
§2矩阵的运算
从37页第6行到38页倒数第四行可以不看,42页“六、共轭矩阵”可不看
特别强调例9很重要,掌握结论
§3逆矩阵 重要
习题二:第3、13题不做,2、4只需记结论;其余必做
第三章 矩阵的初等变换与线性方程组
定理证明部分可不看,70页例8、例9不需要,其余全看
习题三:1、2、4、5、6、7、8、9、10、12、15、16、17、18
第四章 向量组的线性相关性
§1例3不看;§2全看;§3例8不看,例10不看;§4重点看
习题四:做第1至7题,第9至13题;第20至23题;第26至28题
概率论与数理统计部分(浙大四版)
淅大四版第一章:看第1、2、3、6节 习题一:第2、3题
浙大四版第二章(重点) 37页泊松定理不看,其余都看。
习题二:第2、3(1)、7、8、9、12、19、20、21、23、24、25、33
第四章
§1数学期望
例2,例5不看;95页倒数第二段起至本节最后不看
§2方差 105页例8起至本节最后不看
习题四:5、6、7(1)、11、14、20、22
说明:以上整理内容来自高联林夏归纳。