瞬时转动中心和弦转角，是位移法求解含牵连位移的结构时，用来计算典型方程主、副系数以及自由项的有效方法。下面以一道牵连位移的入门题为例子进行讲解，这是很多初学者很头疼的问题，目前大多数参考书都没有用弦转角和瞬心来求解，而是用位移的几何关系来分解，这样不但速度慢而且要是对位移感觉不好的人来说很容易做错，可以与我所讲解的方法进行对比，增加自己的做题技巧！

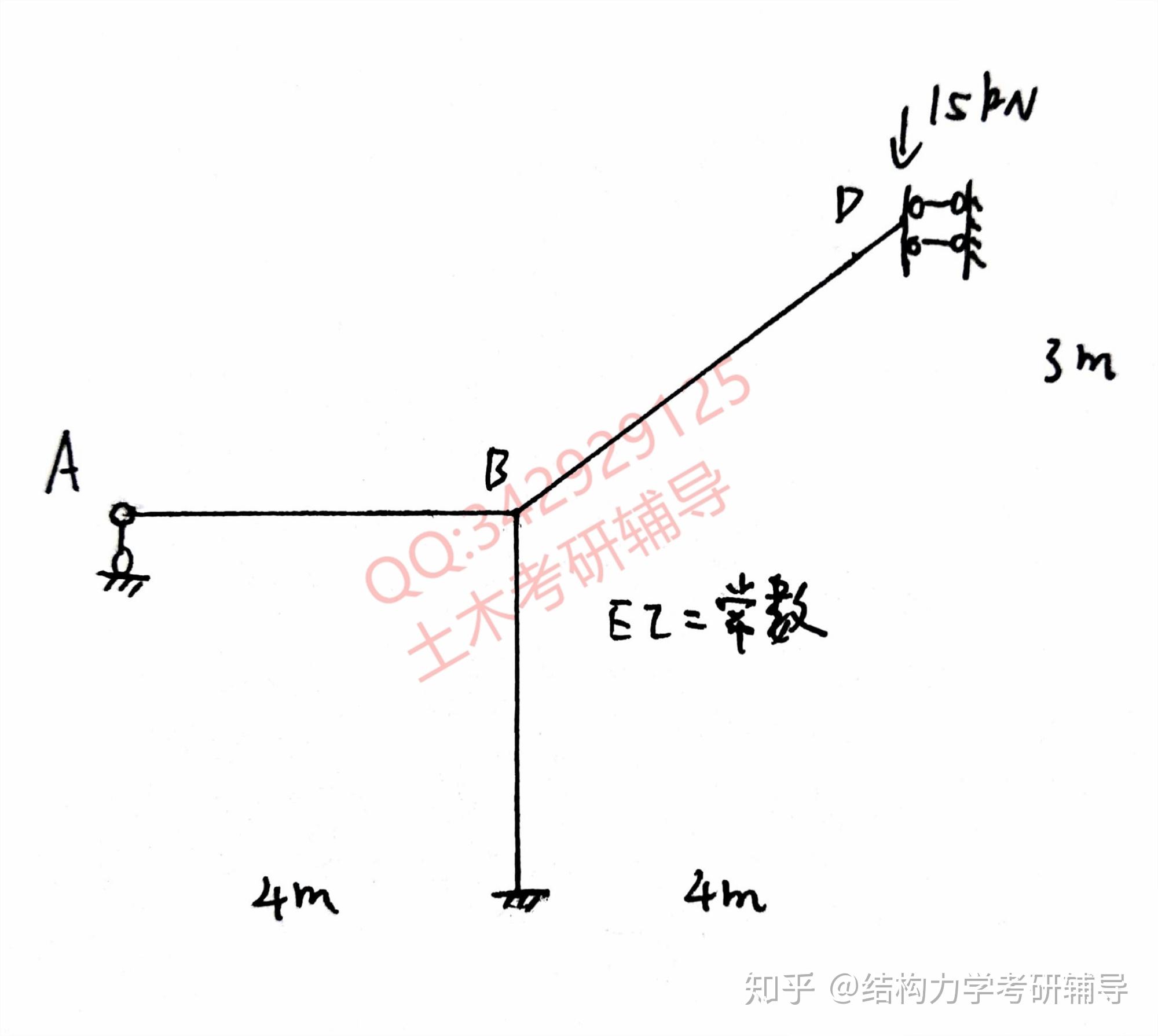
1.用位移法求解图示结构的弯矩图，各杆 常数，杆件长度如图所示。

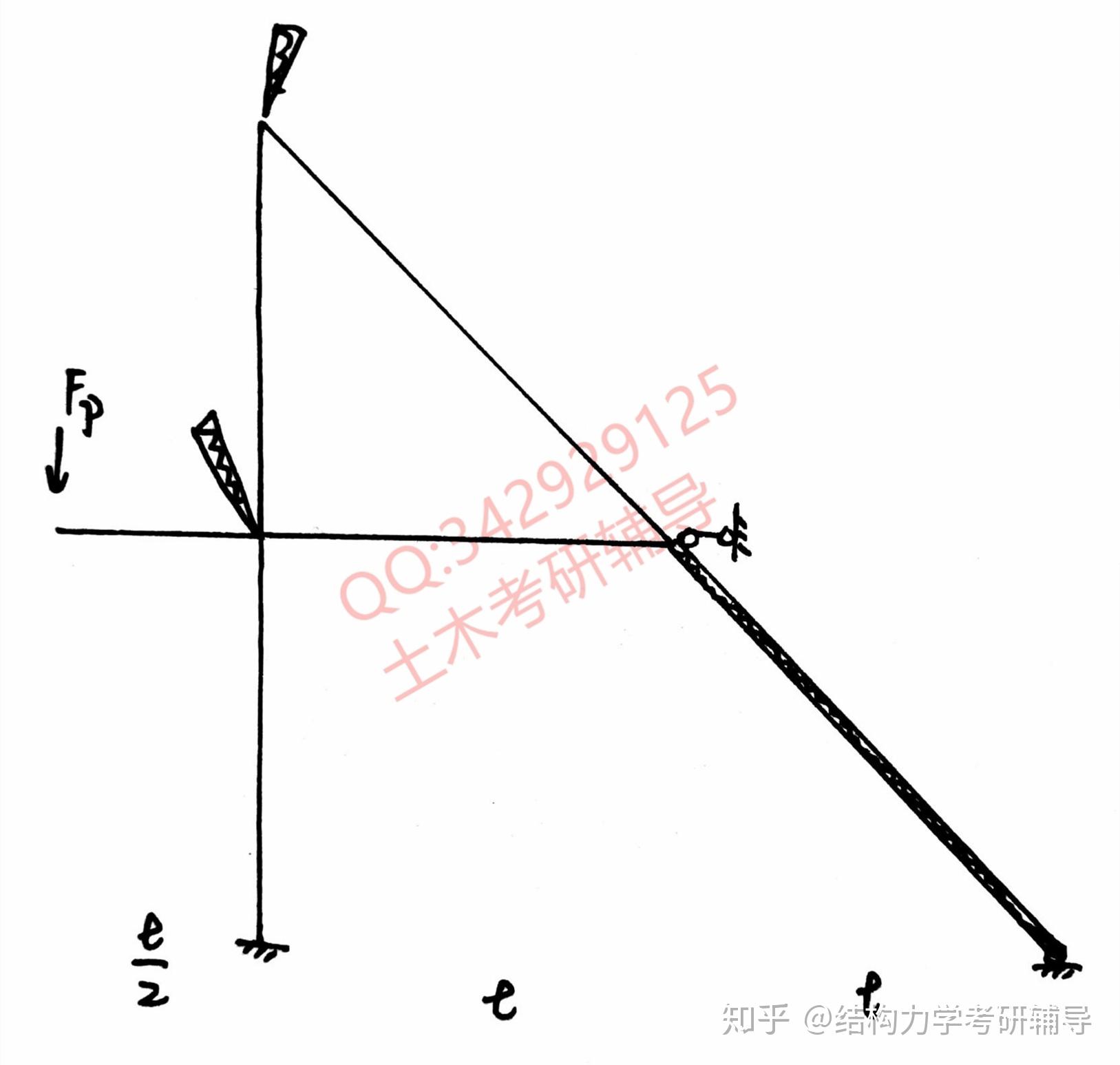
解：这题看似很简单实际上还是有点综合的，首先判断基本未知量就很容易遗漏线位移。观察结构很容易发现点和点的线位移是牵连的，约束一个即可。所以，基本结构为下图所示：

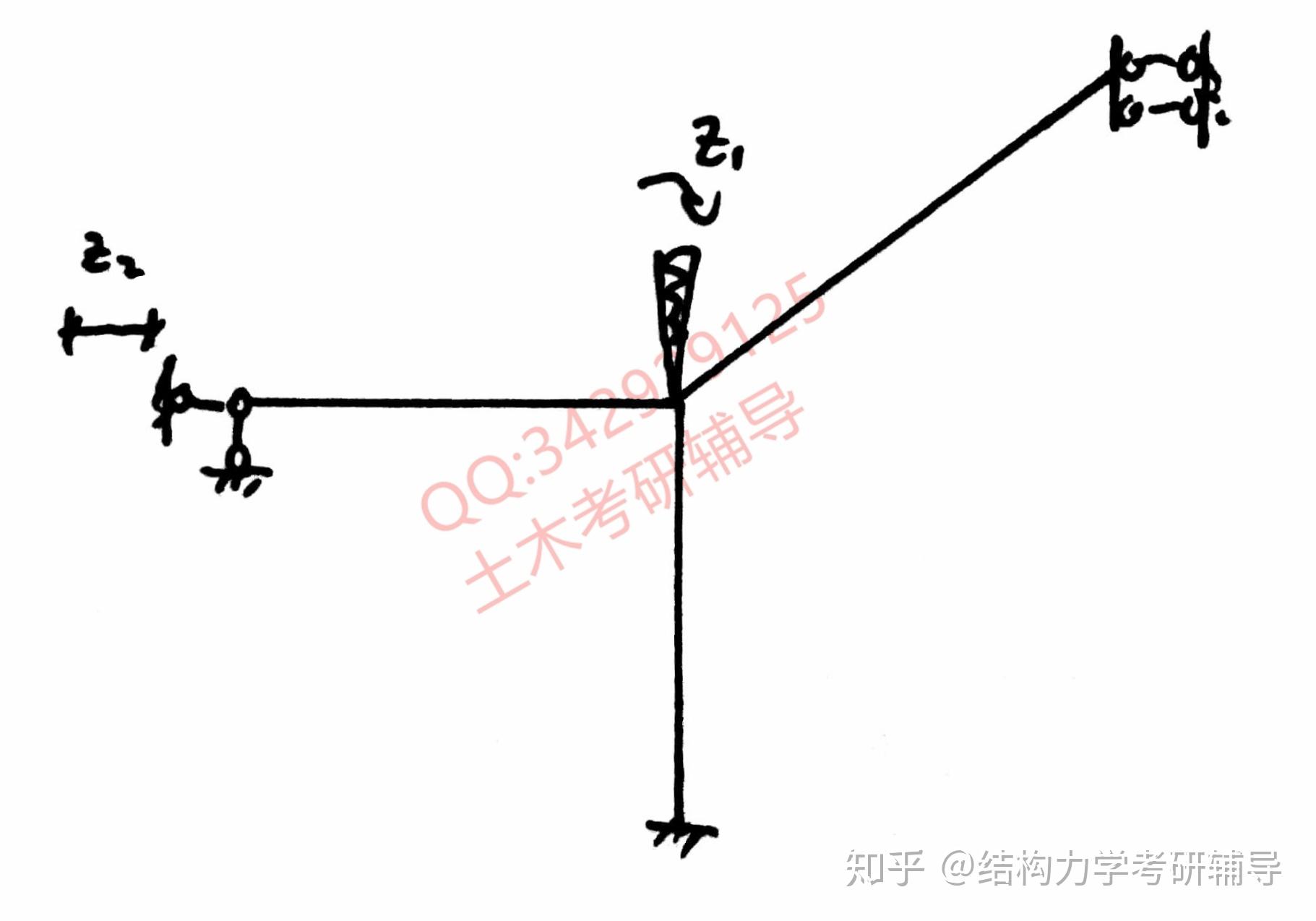
对大多数人来说，图都没问题，那么图可能稍微有点问题，下面就用上面提到的两个概念来入手。首先对于两点线位移具有以下关系

那么其位移关系是利用瞬心的概念是很好确定的，再加上弦转角就就能一步解决，看下图解答步骤：

之后求出、图：

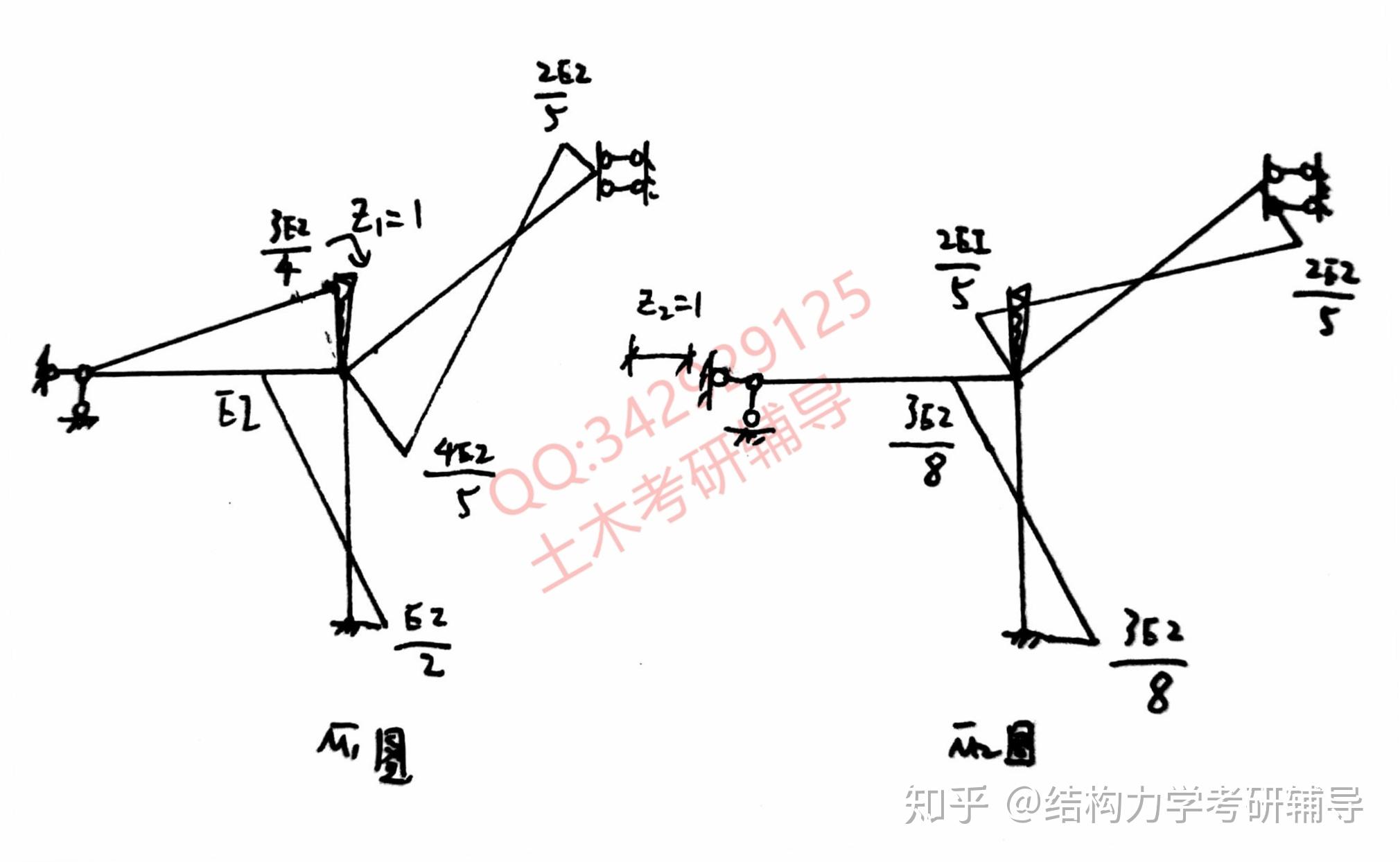
下面来求，一般来讲都是瞬心取矩，这样轴力就通过瞬心，避免轴力带来的弯矩的影响。以下为求解过程：

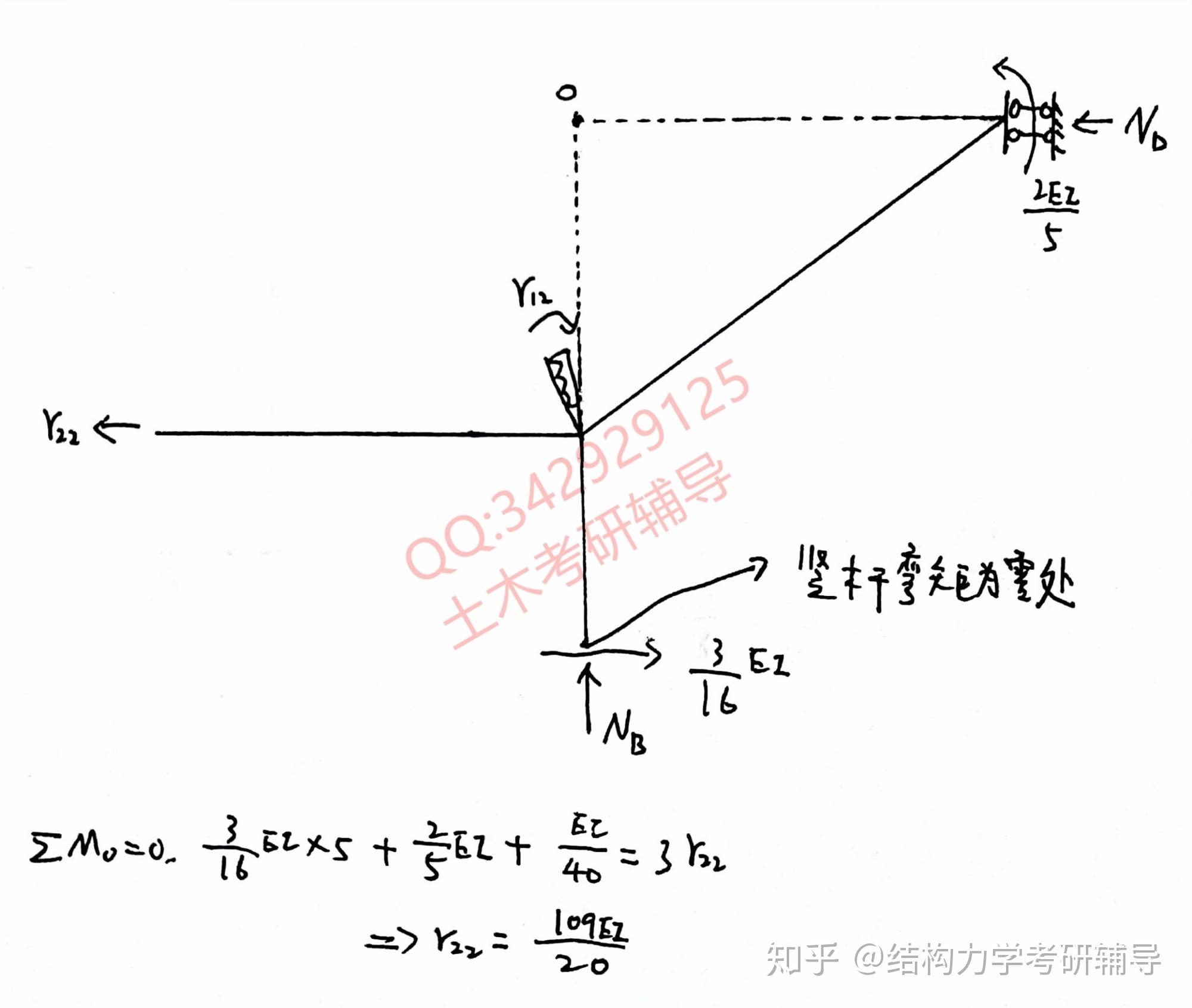
那么对于图也是一个比较容易错的点：

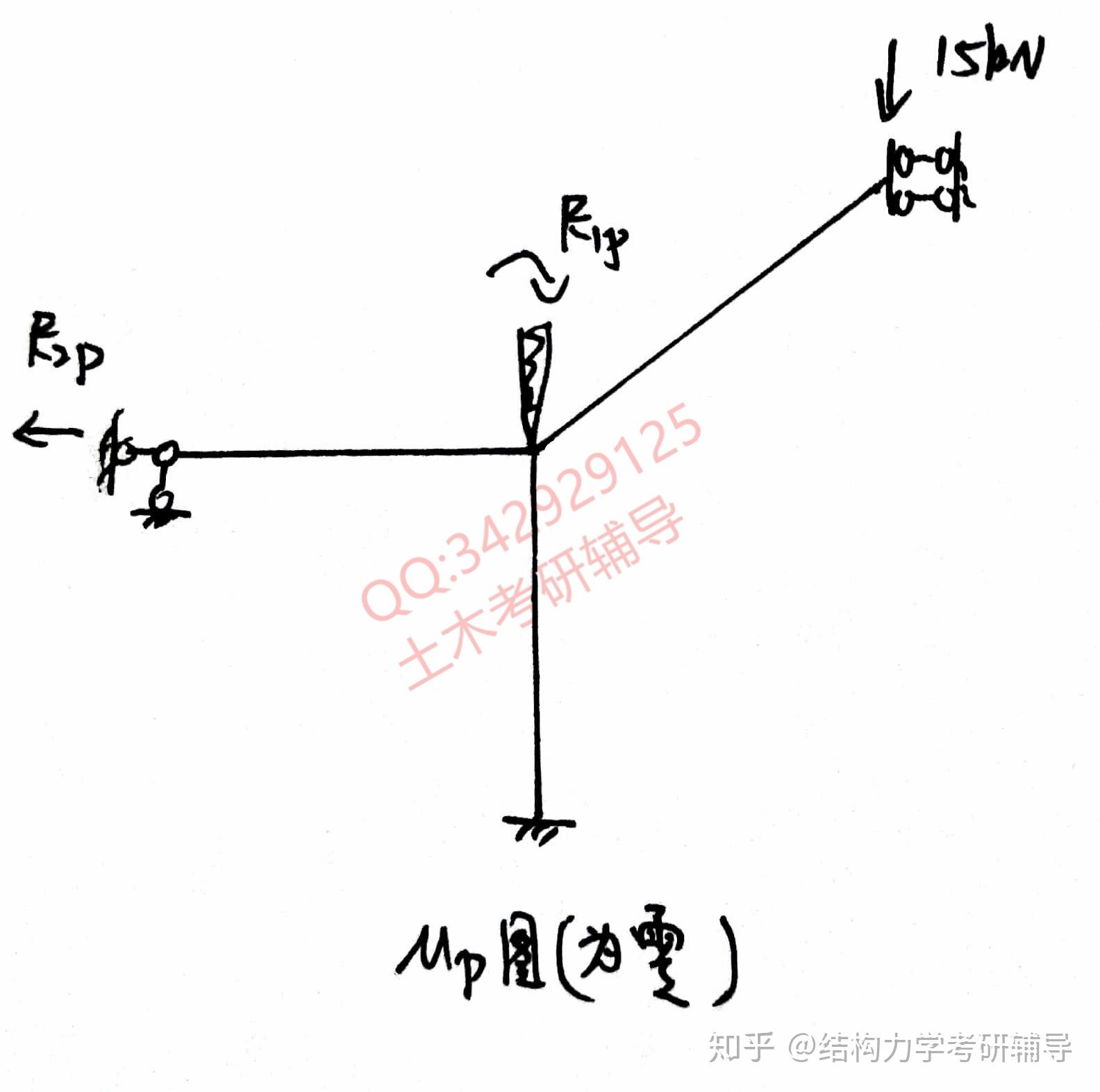
图是没有弯矩的，因为对与滑动支座来说，他是不能滑动的，不能发生线位移也不能发生角位移，等效成固定端，所以无弯矩，则为0， 用 的求法即可求出，最终弯矩图为：

上题为二连杆问题，下面介绍三连杆问题，这题的求解过程更为复杂，是斜杆中最难的一类题目，如果这道题你都能做对，那么斜杆与牵连位移的考点你就已经完全掌握了！前方高能：

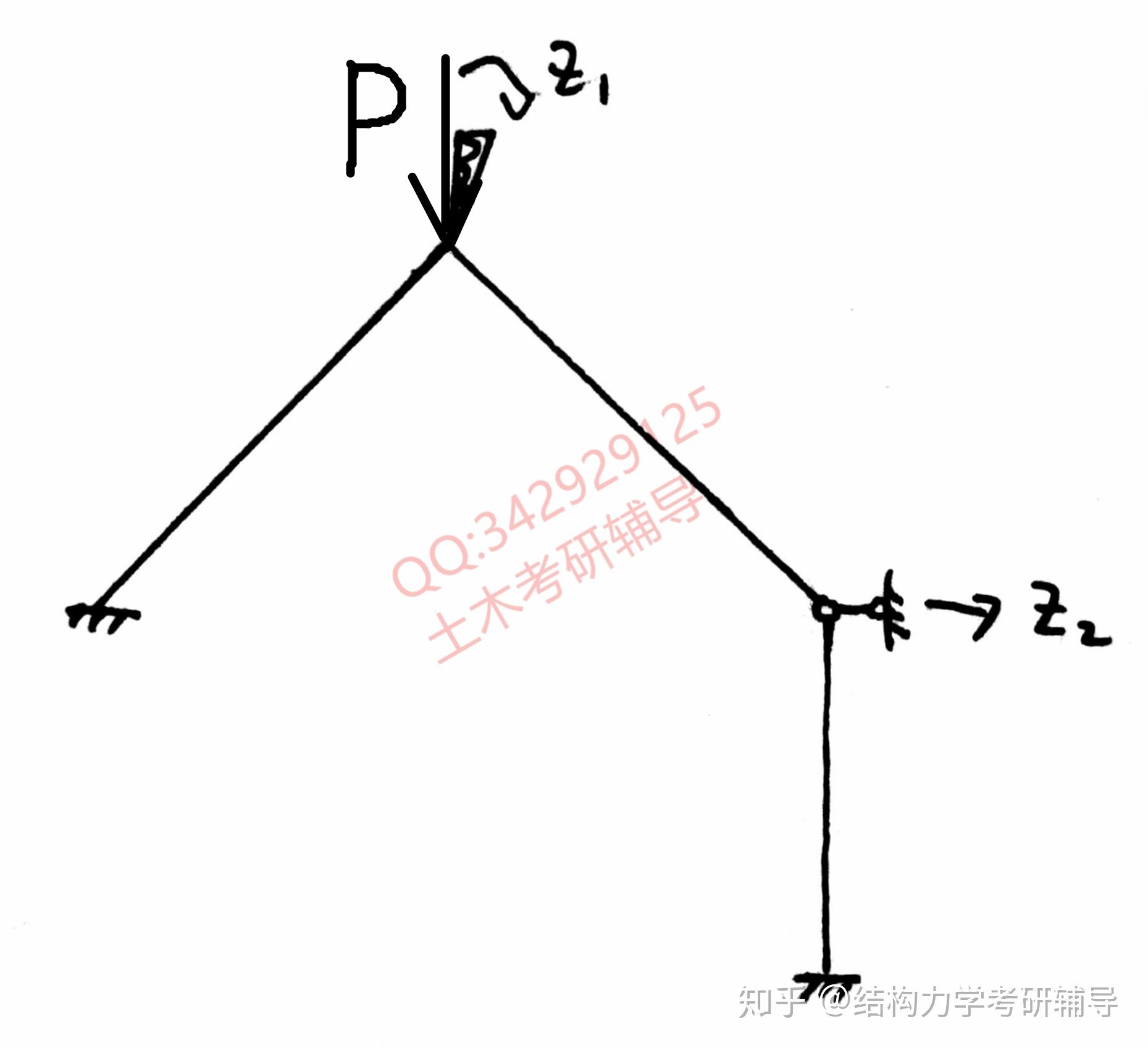
2.列出下图所示结构的位移法典型方程，各杆 常数。

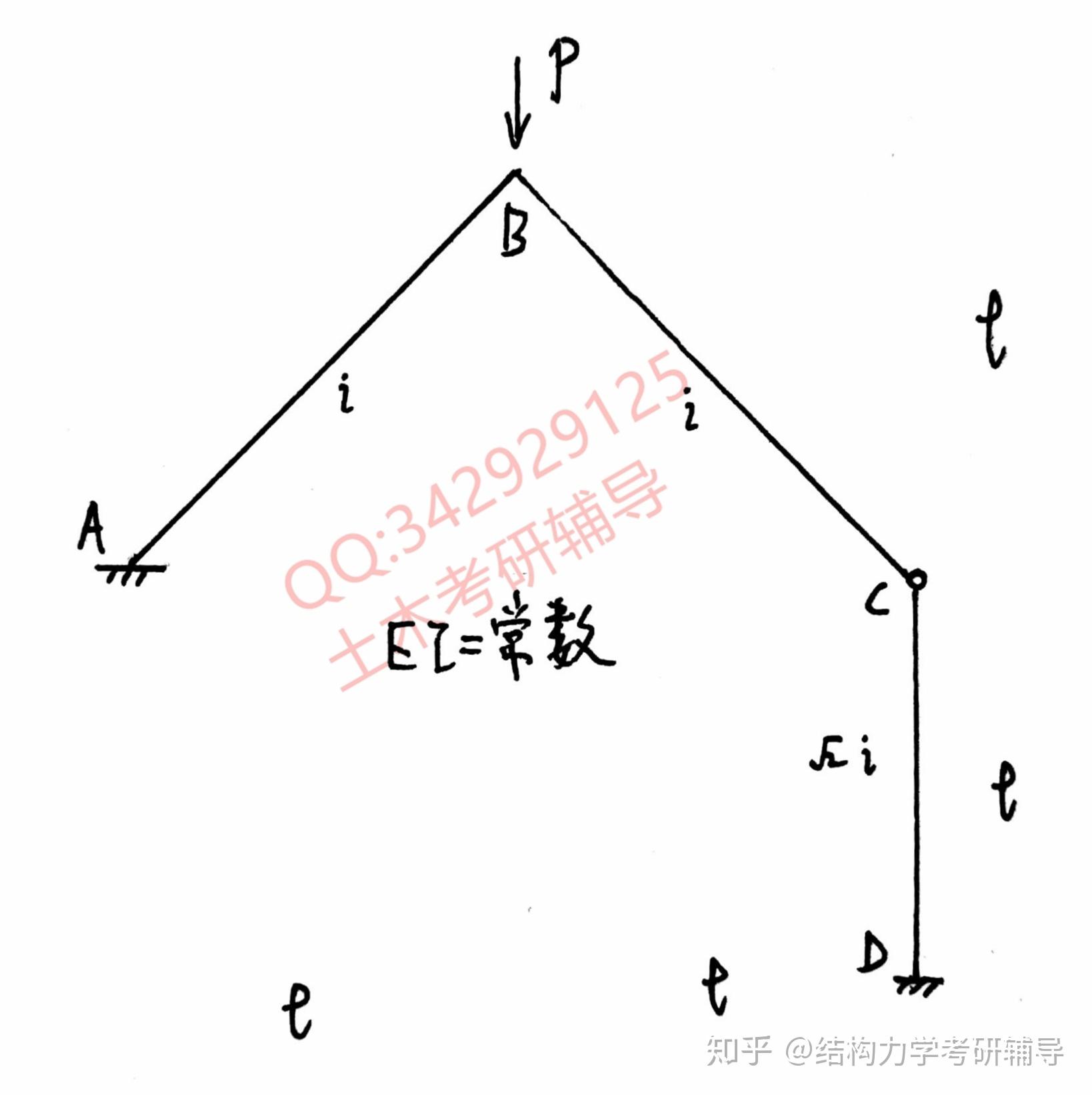
解：很好判断基本未知量为一个线位移，一个角位移，基本体系如下：

图好画：

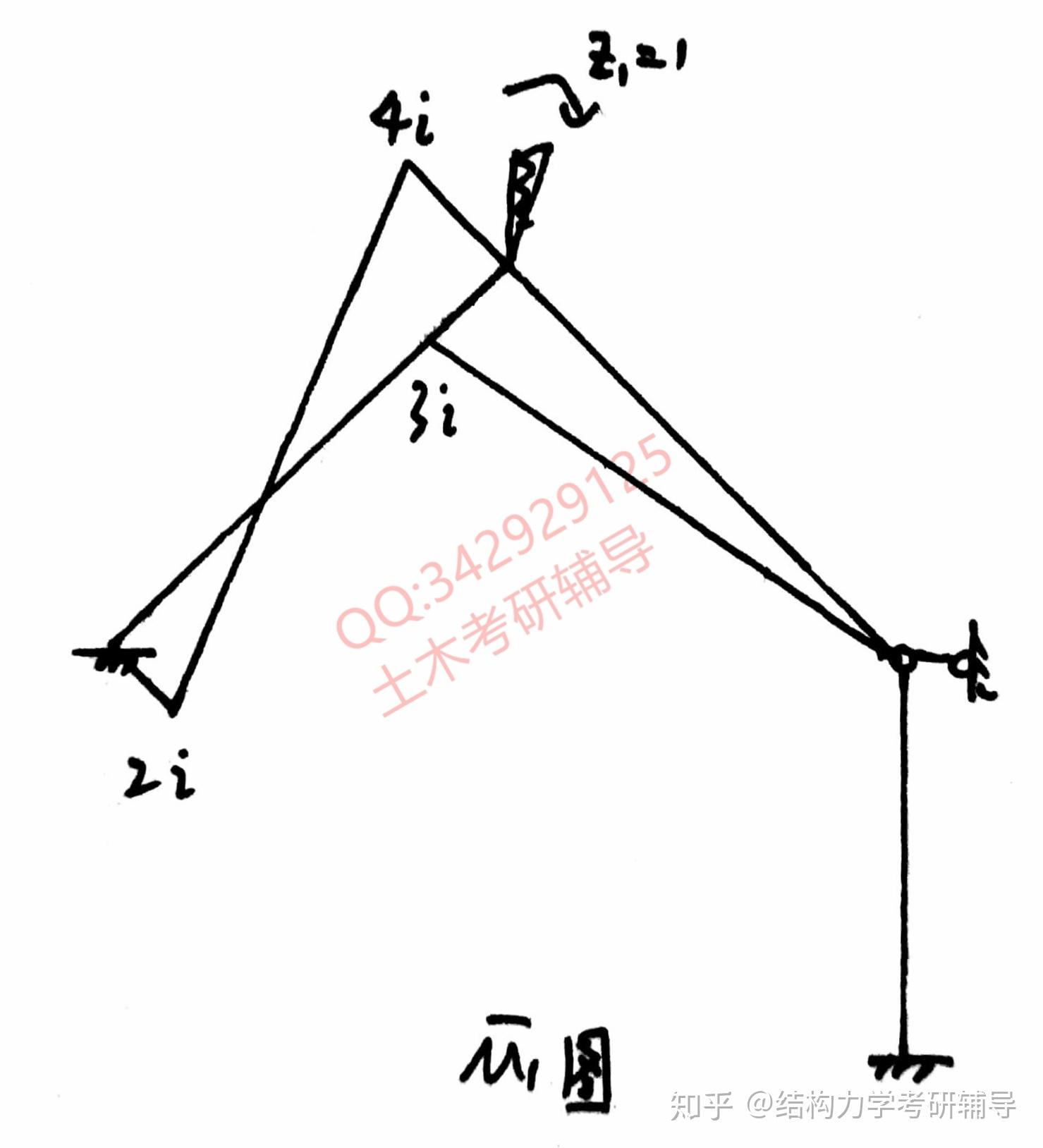
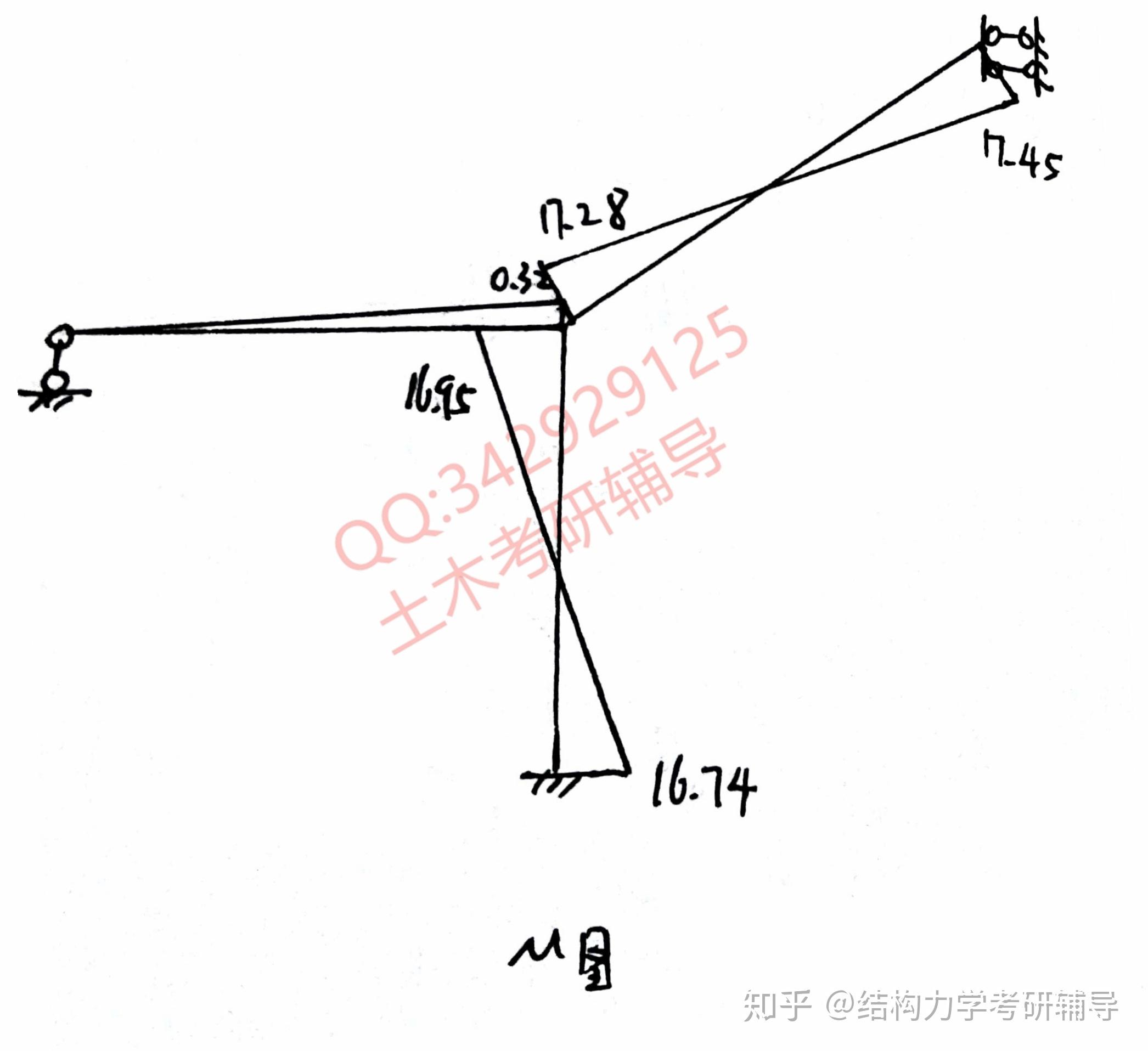
那么 图就需要做简单分析了：

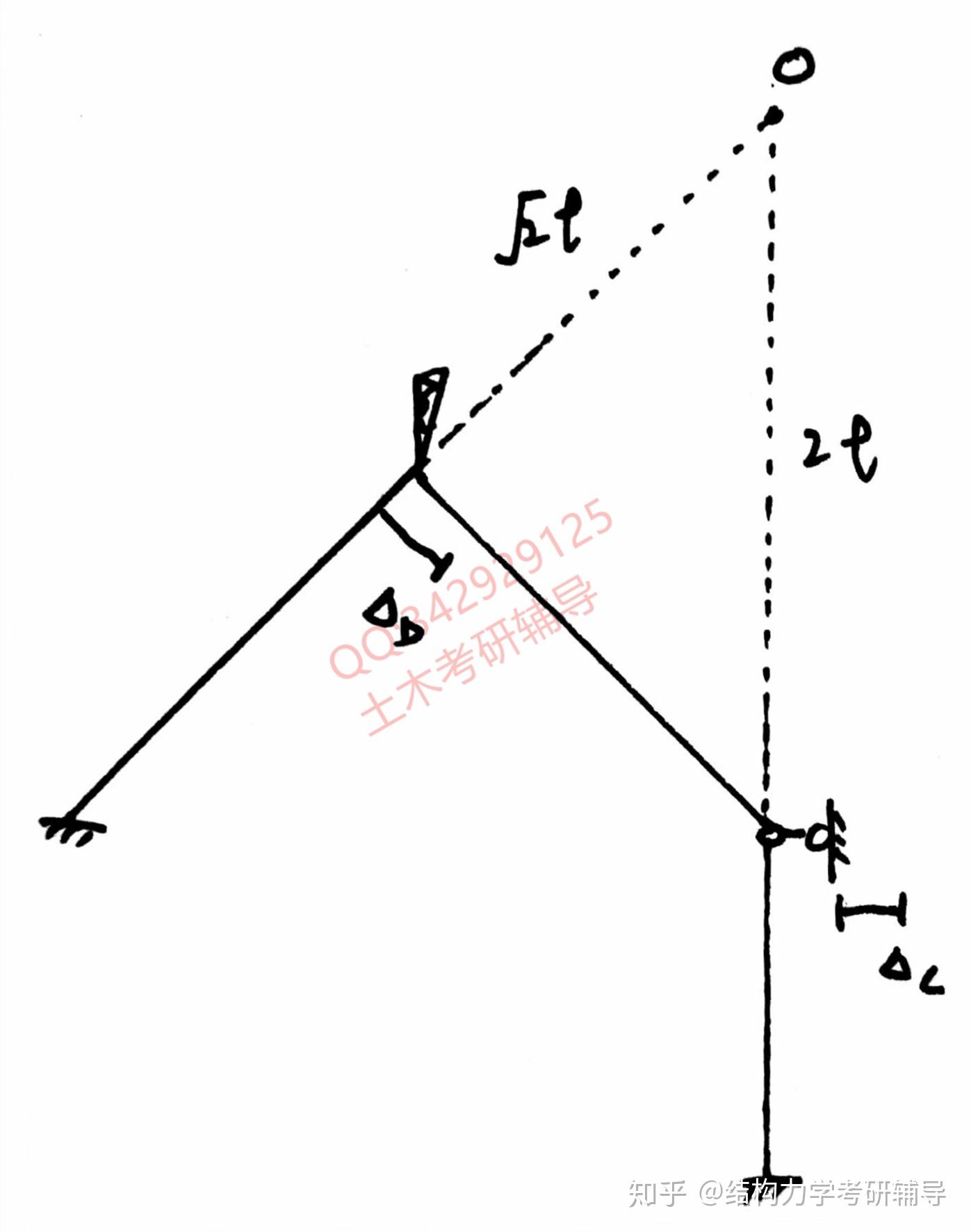
首先位移关系和，和速度瞬心要找对，不然都是空谈，找出后，运用杆端弯矩和弦转角的关系即可算出中间斜杆弯矩，运用位移和半径的关系即可算出左端斜杆弯矩，具体如图所示：

图也是无弯矩的：

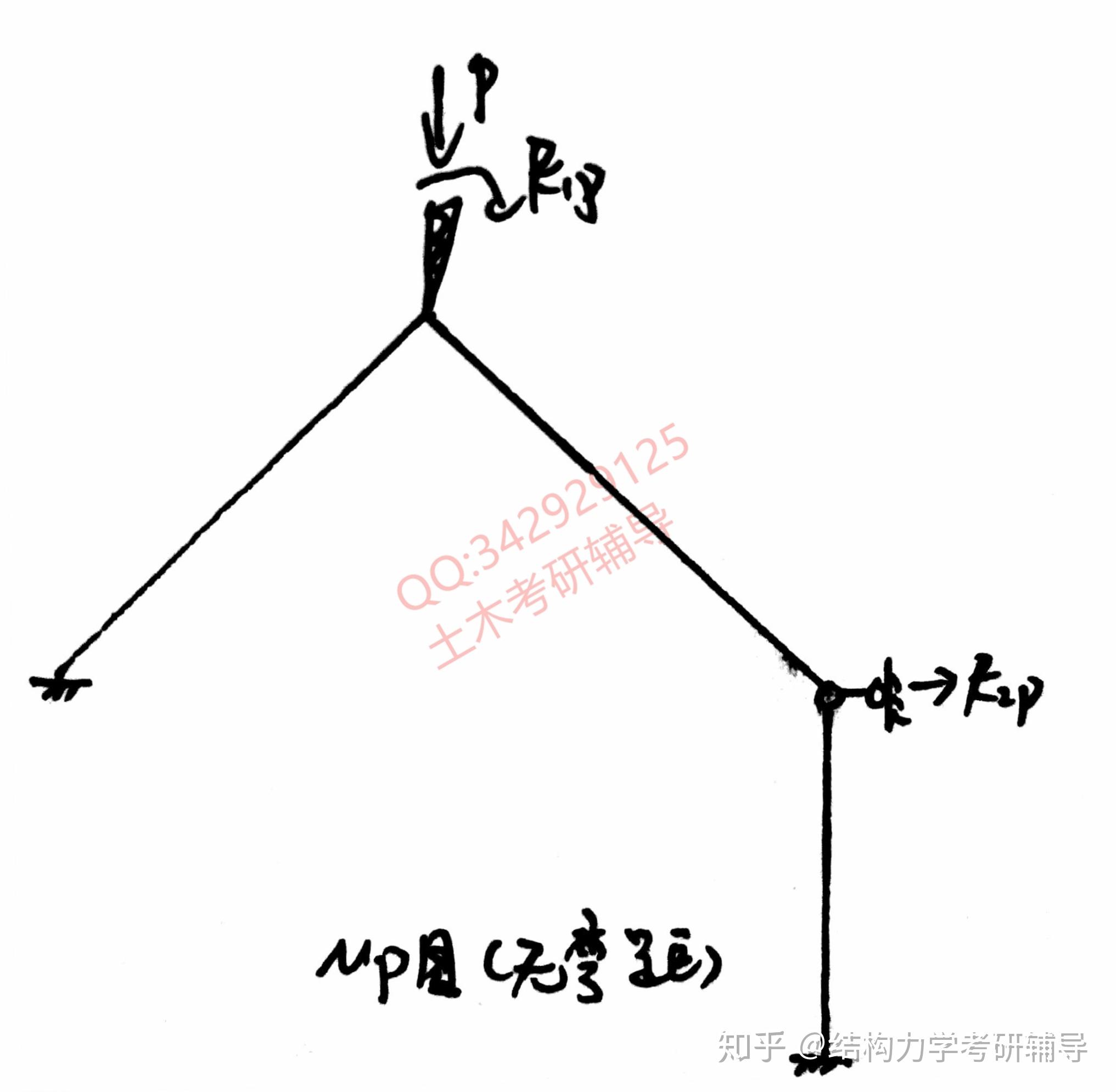
对于 和 利用前面的求法即可顺利求解：

求解过程：

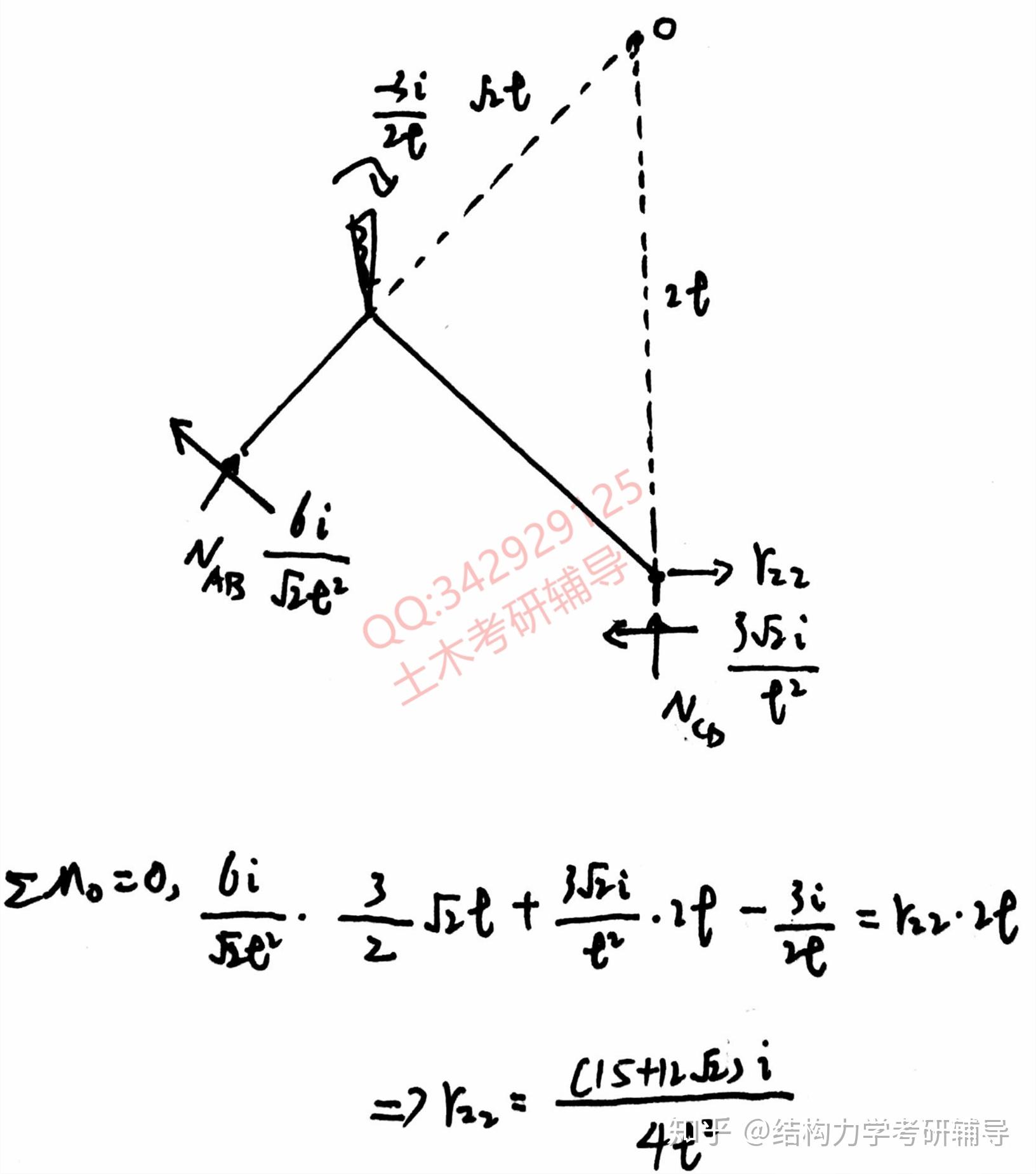
求解过程：

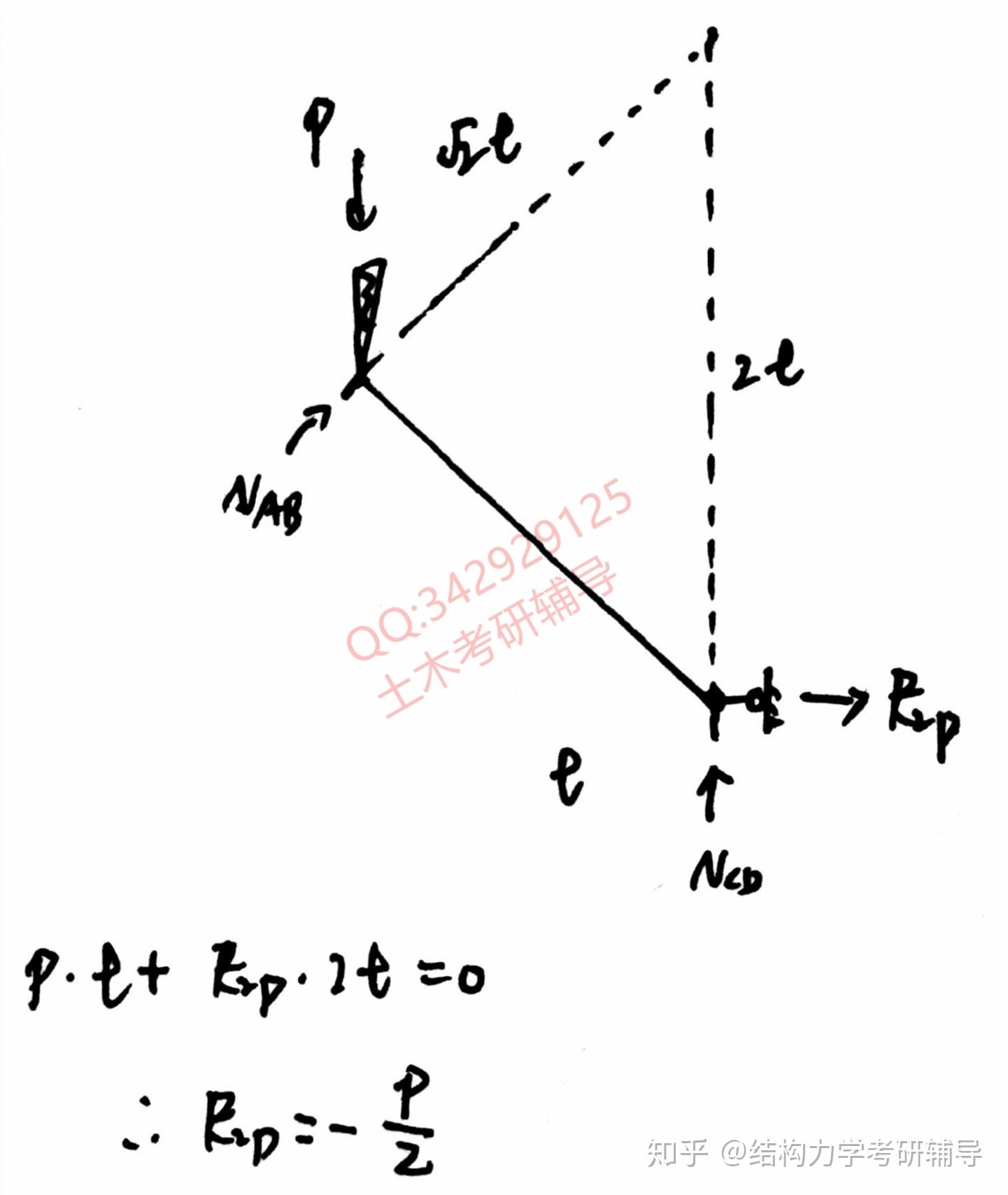
最终所有系数和自由项如图所示：

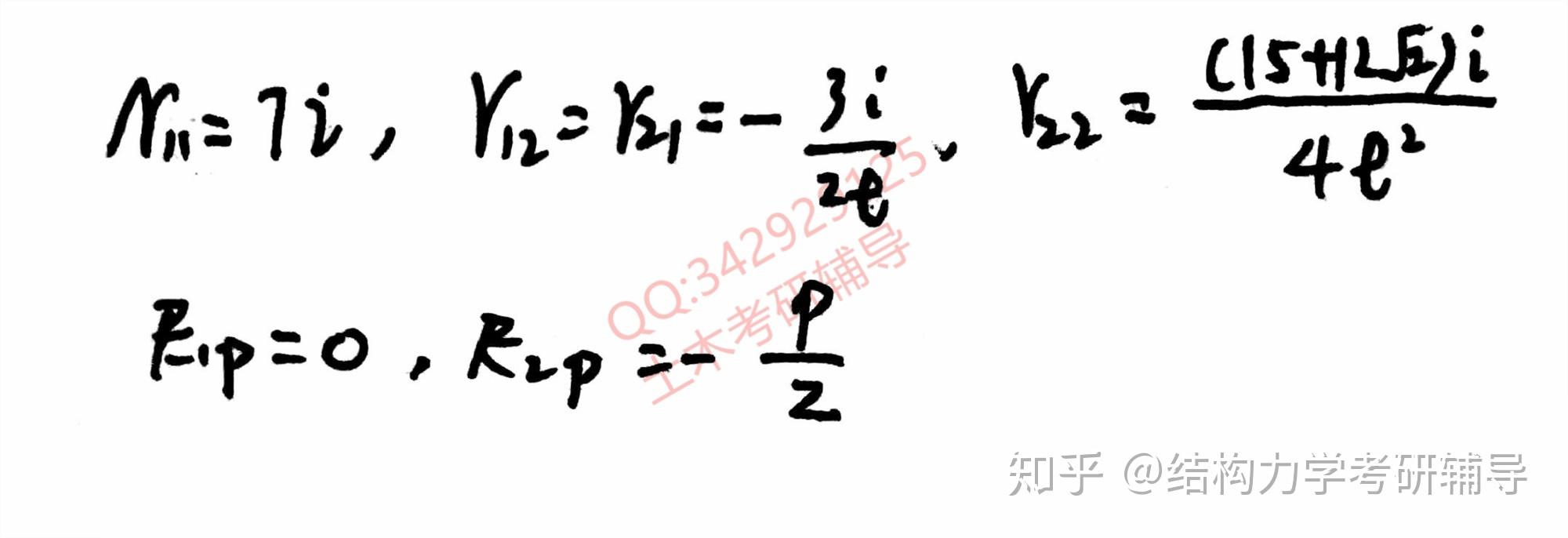
最后留下四连杆问题，请期待下回分解。更多精彩请关注